转自：http://blog.sina.com.cn/s/blog_7445c2940102x3x4.html
侵删

其实，在上高中的时候我们就已经对非线性优化的求解方法了然于心了。可见，非线性优化并不是我们想的那么困难，只不过在后来由于学习了大量的新知识，而迷失其中。你可能不相信，那么让我们一同回到高中的数学课上。数学老师给了如下的问题：

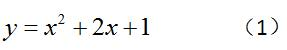
?如何找到上面这个函数的最小值？相信你很快的就能想起上面这个问题的解法，并且求出上面这个函数的极值。而至此，我们已经解决了一个非线性优化的问题。?为什么这么说呢？请看下面的公式：?

当这个公式中的f(x)是一个非线性函数的时候，上面的问题就是一个非线性优化的问题。?也就是说，非线性优化问题是针对一个非线性函数求最值的问题。那么，再让我们回过头看一看数学老师出的问题，这不就是一个非线性优化问题吗？?而且，求解方法也很简单，就是对函数求导，再令导数为零，我们就找到了极值点。可见，非线性优化并不是一个高不可攀的山峰。?

那么，我们是否可以对所有的非线性优化问题，都可以用上面的解法呢？很遗憾，对于很多情况，通过导数为零求解析的求出极值点，是做不到的，如下式：

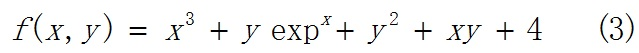
我们对x,y分别求偏导，得到：

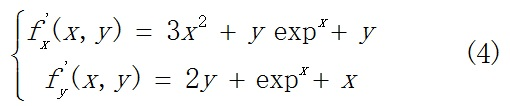
我们很难直接的从上面的式子中，求出导数为0的点。一方面，是因为该函数已经不是初等函数。另一方面，是因为增加了未知数（变量）的个数。我们重新写一下公式（1），如下：?

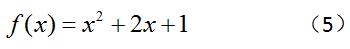
可见，这个函数是一个单变量的非线性函数，而且极值点只有一个。即使，增加x的幂次方，不过是增加了几个极值点，我们还是可以通过之前的办法，只不过将每个极值点的值都带回方程，就可以找到整个函数上的最小值。无论，这个一维函数如何复杂，都可以画在一个二维坐标中，如下：?

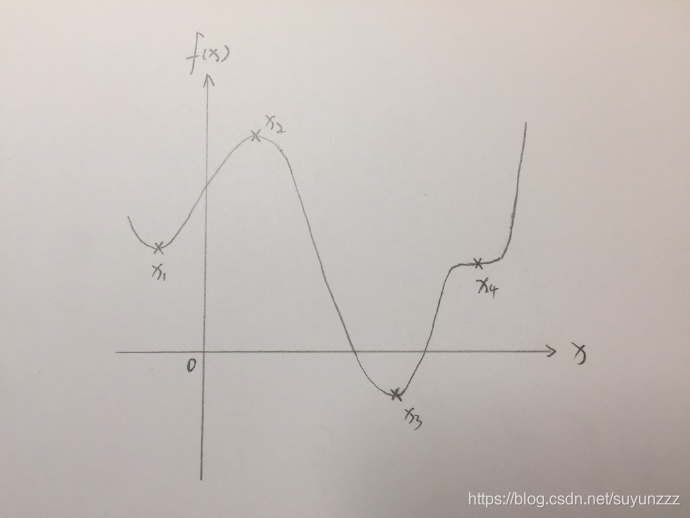
上图中，极值点1和点3是最小值点，点2是最大值点，而点4既不是最大值点，也不是最小值点。通过比较我们知道，点3是全局最小值点，而点1是局部最小值点。

但是，如果再增加函数的变量个数会发生什么呢？比如，只再增加一个变量y，此时函数变为f(x,y)，而这个函数在x和y的方向上都有多个极值点。这时，我们还能将这个函数表示在三维坐标系下，如下：?

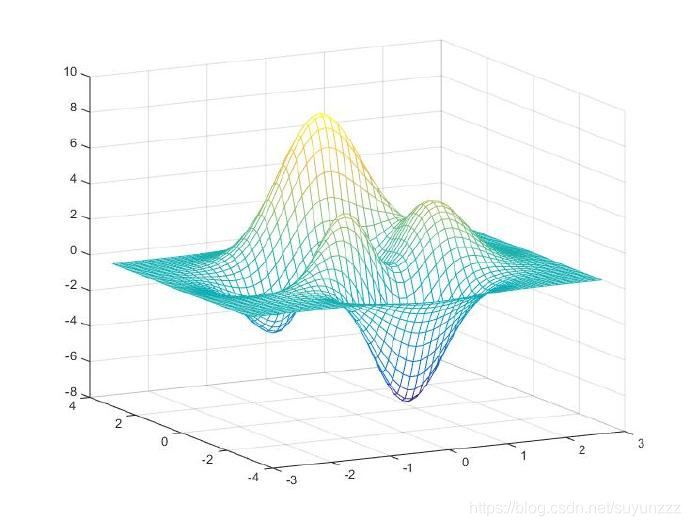
此时，极值点的分布就比一维的情况复杂了许多。当变量个数继续增加的时候，极值点的个数会成几何倍增加，显然也就无法通过求解出所有极值点再比较大小的方法，实现对问题的求解。?

上面的方法是一种比较贪心的解决方法，希望直接找到问题的解。俗话说，饭得一口一口吃，不能一口吃个胖子。这里要注意的一点就是，虽然我们不能直接找到函数值为零的点。但是，非线性函数的导数是存在的，也就可以计算出每一点的导数。也就是说，既然不能直接找到极值点，我们就应该一步一步的逐渐逼近函数的极值点。?

我们将原问题找f(x)的最小值（此处x为n维向量，不是一维的），变为找到f（x+Δx)的最小值，再依此迭代多次，逼近f(x)的最小值。此时，x变为已知，而未知是Δx的大小（当然也可以理解为方向，因为n维向量表示了一个方向）。也就是说，我们希望找到一个Δx，使得函数f（x+Δx）在点x处取得最小值。那么，一个自然的想法就是将f(x+Δx)对Δx求导，再另f’(x+Δx)=0就可以找到Δx的值。然而，这其实又回到了上面说的问题，即求f’(x+Δx)=0和f’(x)=0是一样不可求的。那么怎么办呢？?

这就要祭出一个大杀器——泰勒级数展开?（有人称为线性化，其实不太准确。在一阶泰勒的情况下却是是线性的，但是如果加了高阶则不是线性了。）

因为，我们求的f(x+Δx)处于f(x)的邻域中，所以就可以用泰勒级数在点x处展开，如下：?

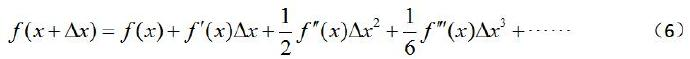
将上式对Δx求导，并令其等于0，得到：

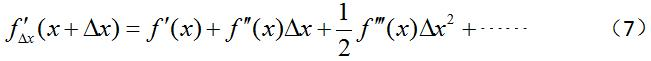
因为上式存在Δx的高阶项，所以还是很难得到上式的解。不过，由于是在点x的邻域内，因此我们可以忽略Δx的高阶项。

（1）当我们只保留一阶项的时候，得到如下式子：?

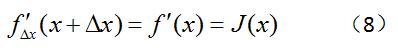
上式中的J(x)在多维情况下，被称为雅可比矩阵，其实就是对f(x)求偏导。接着，一般书就会直接给出增量Δx的大小，如下：?

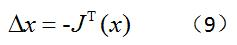
这个过程其实不太好理解。因为，如果从一维的角度理解，那么此处的f’(x)只是一个斜率，按理说斜率的多少跟Δx的值是无关的，只要Δx值不要太大保证在邻域内就可以。所以，直接得出上面的式子就感觉很诡异。?

其实，换一个角度解释上面的式子就很容易理解。这里让Δx等于负梯度，重点并不在于Δx的大小，而是规定了Δx的方向。其实，即使在1维里，我们也可以这么理解，Δx=-k，此处的k只用于提供方向，也就是正负号，而不代表走多远。?对于多维情况更是如此，因为我们需要知道增量的方向，而方向是由Δx各维度大小决定的。其实，一个更清晰的表示应该是将梯度归一化，然后再乘以一个步长系数，如下所示：?

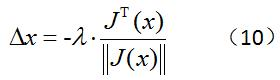
这个方法也就是我们经常听到的——最速下降法。

（2）如果我们保留到二阶项的时候，得到如下式子：?

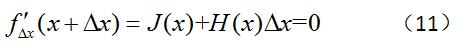
上式中的H(x)被称为Hessian矩阵，而且J(x)和H(x)在点x的值是已知的，所以上式是一个线性方程组。写成矩阵形式如下：?

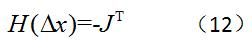
Δx的值可以通过解这个方程得到，求解方法由很多，在此就不再赘述。这个方法，就叫做——牛顿法。

说到这里，你可能会疑惑，既然非线性优化好像通过上面的方法都可以求解，那么为什么还有那么多数学家在研究这个问题。或者说，是不是世间所有问题，都可以通过这个方法求解呢？要想回答这个问题，我们需要重新来审视一下上面的求解过程。?

（1）==其实这个过程有个重要的前提，那就是f(x)是连续可导。如果f（x）这个函数不可导，或者不可微呢？==比如说，在SLAM中需要处理姿态估计的问题。而姿态是通过旋转矩阵和平移向量表示的，这显然是不连续的。但是，由于旋转矩阵是一个李群，那么我们可以将其映射到其李代数上。而且，李代数是可以求导的。所以我们就还可以利用非线性优化的方法对姿态进行估计。也就是说对于不连续的函数，我们可以想办法将其变得连续，从而继续用这种方法。?

（2）上面的解法求得的只是局部最优解，而不能确定是否是全局最优解。因为，这种方法可以说是一种“近视眼”的方法，它只看到下一时刻，在邻域内的最小值，而不能全局的寻找。所以，很容易陷入到局部最优中，或者说最终求出的最优值是跟初始位置极度相关的。即使初始值在同一个未知，也很有可能落入到两个不同的局部最优值中，也就是说这个解是很不稳定的。所以，如何解决这个问题，至今仍然存在很大的挑战。

比如凸优化就可以在一定程度上解决这个问题。凸优化的思想是，如果局部最优就是全局最优，就不存在这个问题了。那么如何将一个非凸的问题转换成凸的呢？或者什么问题就是凸的，什么是非凸的呢？

在此，只是粗浅的举了两个例子，其实非线性优化中存在的问题还有很多很多。而且我们在这里只讨论了无约束的情况，而优化问题真实情况往往是存在对变量的约束的。本文只是希望破除我们心中对非线性优化的恐惧，勇敢的迈进非线性优化这道大门。